Geometria analitica: che cos’è

Che cos’è la geometria analitica? Quali sono le applicazioni? E in quali corsi di laurea viene studiata in modo approfondito? In questo articolo lo staff della Università Niccolò Cusano di Lecce intende rispondere a tutti questi quesiti, avvicinando gli studenti a questa materia.

Definizione di geometria analitica

Iniziamo subito con il darne la definizione: la geometria analitica, o geometria cartesiana, studia le figure piane ed i luoghi geometrici utilizzando le coordinate cartesiane del piano. Con l’interiorizzazione di questo studio si comprenderanno gli enti geometrici del piano sotto un punto di vista prima di tipo analitico e poi algebrico e questo è fondamentale in tutti i livelli dello studio della matematica.

Il piano cartesiano

Iniziamo subito con il dare la definizione dello “spazio” dove si rappresentano le figure geometriche piane. Si tratta di un piano in cui ciascun punto viene individuato mediante una coppia di numeri reali disposti su ascissa ed ordinata.

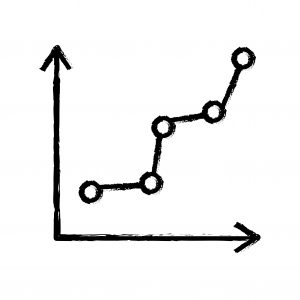
Questo sistema di coordinate è in grado di definire una rappresentazione grafica ed analitica di una figura. Per disegnare un piano cartesiano è sufficiente tracciare due rette orientate e perpendicolari tra loro (l’asse delle ascisse o delle x sarà quella orizzontale mentre l’asse delle ordinate o delle y quella verticale). Dunque i numeri reali di cui parlavamo sopra saranno positivi  verso l’alto sulle ordinate e verso destra sulle ascisse, partendo dal centro; nell’altro verso saranno negativi.

Dunque le figure fondamentali possono essere identificate come punto, retta e piano.

La retta: definizione e formule di riferimento

Arriviamo quindi alla definizione di retta: un insieme infinito di punti allineato nel piano cartesiano. È quindi possibile individuare qualsiasi tipo di retta con una equazione delle incognite x e y. Questa equazione descriverà la retta come un luogo geometrico e si può presentare come di seguito:

y = mx + q

dove x e y sono variabili mentre m (il coefficiente angolare) e q (la quota all’origine della retta) sono costanti.

Formule di circonferenza e cerchio

Ma non solo la retta può essere disegnata sul piano cartesiano bensì anche le circonferenze. Nello specifico, la circonferenza p quel luogo geometrico formato da punti equidistanti da un punto fisso, detto centro della circonferenza.  La distanza tra qualsiasi punto ed il centro viene chiamata raggio (r).

Date queste definizioni è possibile fornire anche quella di cerchio: un cerchio p la regione del punti del piano interni alla circonferenza.

Le formule della circonferenza nel piano cartesiano sono una estensione di quelle già riportate nella geometria euclidea. Tenendo presente il centro della circonferenza  con la formula:

C = (xc, xc)

unitamente alla la misura del raggio, possiamo esprimere l’equazione della circonferenza come di seguito:

(x-xc)2 + (y+yc)2= r2

Da ciò possiamo dedurre anche le formule del cerchio utilizzando una disequazione:

(x-xc)2 + (y-yc)2 < r2

Inoltre, nel piano cartesiano possono essere costruite anche parabole, ellissi e coniche

Quando si studia la geometria?

Arriviamo ora a parlare delle applicazioni pratiche della geometria analitica o meglio, specifichiamo il quali corsi di laure questa diventa una materia cardine per l’apprendimento (e, dunque, in seguito parte integrante della professione che si andrà a fare).

La Unicusano di Lecce mette a disposizione degli studenti un percorso di studio telematico in Ingegneria Civile (laurea triennale). Questo corso di laurea  realizza un percorso formativo orientato a fornire una preparazione metodologica, che utilizzi tutte le conoscenze di base, matematiche, fisiche, chimiche, informatiche, e le conoscenze delle materie specifiche caratterizzanti dell’Ingegneria Civile. I risultati di apprendimento attesi, quindi, riguardano – tra le altre – conoscenze di base incentrate sulle discipline dell’analisi matematica, della geometria e della fisica generale per essere in grado di interpretare e descrivere i problemi propri della materia.

La geometria nel corso di laurea online in Ingegneria Civile

Dunque, l’insegnamento di geometria è basilare nel primo anno dei del corso di studi triennali in Ingegneria Civile (ma anche in Ingegneria Industriale). Il programma proposto dai docenti della Unicusano verte sui seguenti argomenti:

• spazi vettoriali R n
• elementi di calcolo matriciale (somma, prodotto per uno scalare, trasposizione, rango, determinanti, inversione)
• tecniche di calcolo (rango, determinanti, risoluzione di sistemi lineari)
• problemi di natura geometrica riguardanti enti fondamentali del piano (punti, rette, curve) e dello spazio (punti, piani, rette, superfici)

L’insegnamento di Geometria si pone i seguenti obiettivi formativi:

• illustrare la teoria elementare degli spazi vettoriali R n
• illustrare le basi del calcolo matriciale;
• illustrare la discussione e la risoluzione di sistemi lineari;
• illustrare la teoria di base degli operatori lineari su R n
• illustrare le tecniche fondamentali della Geometria analitica piana;
• illustrare le tecniche fondamentali della Geometria analitica dello spazio.

Detto questo è immediato pensare che al superamento del corso, sarà in grado di risolvere problemi di algebra lineare utilizzando la teoria delle matrici: in particolare, la formulazione matriciale della teoria degli operatori lineari permetterà allo studente di applicare le tecniche dell’algebra lineare apprese allo studio degli operatori e alla loro diagonalizzazione.

Inoltre, la conoscenza della rappresentazione analitica del piano e dello spazio euclideo permetterà allo studente di applicare le tecniche di base dell’Algebra lineare acquisite alla ricerca e allo studio delle equazioni dei luoghi geometrici, trasformando un problema di natura geometrica di livello semplice o medio in un problema analitico da risolvere con strumenti algebrici.

In seguito, gli studenti potranno anche imbattersi nell’esame di Complementi di geometria. In questo caso saranno trattati argomenti quali la teoria generale degli spazi vettoriali sopra il campo reale, che generalizza molte delle nozioni studiate durante il corso di Geometria.

Una particolare attenzione viene rivolta allo spazio vettoriale euclideo dei tensori, definiti a loro volta sullo spazio vettoriale euclideo dei vettori geometrici. Questa parte si chiude con lo studio delle forme quadratiche su R n e la loro riduzione a forma canonica, strettamente legata alla teoria degli operatori lineari simmetrici.

La seconda parte del programma, invece, prevede lo studio della rappresentazione cartesiana di curve e superfici dello spazio – circonferenza, sfera, coni, cilindri e superfici di rotazione.

La terza parte – che richiede padronanza del calcolo vettoriale – concerne la geometria differenziale delle curve e delle superfici nello spazio, ovvero lo studio di proprietà locali di curve parametrizzate (curvatura, torsione) e di superfici parametrizzate (curvatura gaussiana e curvatura media) per mezzo degli strumenti del calcolo differenziale, rispettivamente in una e due variabili.

Vi ricordiamo che tutti i corsi di laurea della Unicusano di Lecce si svolgono in maniera telematica e quindi possono essere autonomamente seguiti da casa con l’ausilio di video-lezioni che è possibile trovare sulla piattaforma dedicata. Per ulteriori informazioni è possibile contattare lo staff della Università Niccolò Cusano al numero 800 98 73 73.